Histogram
단일변수 데이터 분포에 대한 요약적 정보를 그래픽하게 보여줌
데이터 중앙(위치), 데이터 퍼짐(범위), 데이터 왜도, 이상치 존재여부, 최빈값 존재여부 등
적절한 분포 모델에 대한 강력한 힌트
Histogram 그리는 법
데이터 값 범위를 일정 크기의 구간(혹은 클래스)으로 나눔
각 구간에 포함되는 데이터 점들의 수를 집계
수직축 : 빈도 / 수평축 : 반응변수
히스토그램의 변형
- 누적히스토그램
- 정규히스토그램
정규화 방법
1) 각 클래스(bin)의 수/전체 데이터수 -> 전체 빈도(높이) 합 = 1
2) 각 클래스(bin)의 수/ 전체 데이터 수 * 구간 크기 -> 전체 면적 합 = 1

code ex)
#데이터: 195 samples in zarr13.csv
df_zarr = pd.read_csv(PATH+'zarr13.csv')
sns.histplot(data=df, x="X", bins=30, stat='count')seaborn 의 histplot 이용해서 히스토그램을 그림
stat : 기본값은 count
- freqency(관측수를 bin 너비로 나눈 값)
- density(히스토그램의 면적이 1이 되도록 정규화)
- probability(모든 bar 의 높이가 1이 되도록 정규화) 로 지정 가능
kde : 파란색 분포곡선을 그릴지 말지 / 기본값은 True
- kde = True 이면 그림
- kde = False 면 안그림
Q : 표본 모집단의 분포 / 데이터의 위치 / 데이터의 범위 / 데이터의 대칭성 혹은 치우침 / 이상치 존재 여부
히스토그램의 여러 패턴
1. 정규형

종모양, 중앙에 빈도 몰림, 좌우대칭, 양쪽 꼬리 부분이 빨리 사라짐
-> Normal Probability plot 으로 정규성 확인
2. 대칭, 비정규, 짧은 꼬리
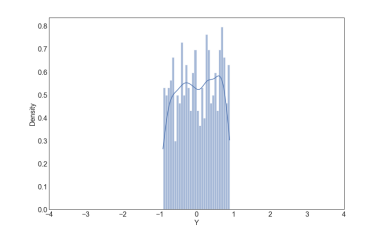
대칭형, 정규형이 아님, 꼬리가 거의 없거나 양쪽 꼬리가 잘린것처럼 생김
3. 대칭, 비정규, 긴꼬리

대칭형, 정규형이 아님, 양쪽 꼬리가 길고 두꺼움
** 꼬리 형태별 확률분포의 특징
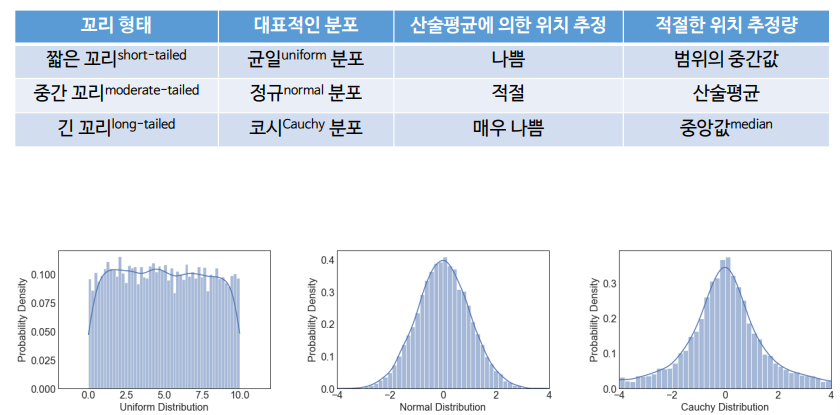
4. 대칭, 쌍봉
대칭형, 봉우리가 2개
1. Run Sequence Plot 혹은 Scatter Plot 이용해서 정현성 검사
* 정현성(sinusoidally) : 정현파(사인파)는 부드러운 반복진동을 설명하는 수학적 곡선. 이러한 형태를 띄는지
2. Lag Plot 으로 정현성 검사. 타원형이면 데이터가 정현적
3. 데이터가 정현적이면, Spectral Plot 을 이용해서 정현파 주파수 측정
정현적이지 않으면, Tukey-Lambda PPCC Plot을 사용하여 데이터에 대한 가장 잘 맞는 대칭형 분포를 결정
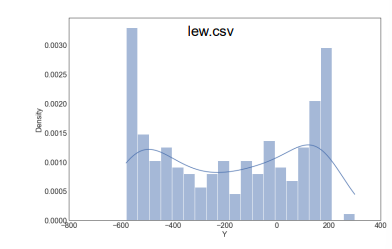
5. 비정규, 치우침(left-skewed, right-skewed)
데이터 치우침 발생 원인
1) 데이터의 상한값/하한값
2) 시작 효과(초기실패, 초기오차, 워밍업)
더 자세한 해석을 위해 표본 평균, 표본 중앙값, 표본 최빈값 계산이 필요
6. 대칭, 이상치 포함
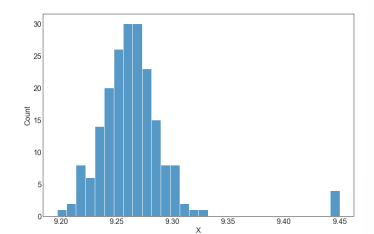
이상치를 그냥 무시하면 안됨 ! 중요한 정보가 있을수도
Box-plot, Grubbs test 사용하면 히스토그램보다 쉽게 이상치 발견 가능
'School > 데이터사이언스개론' 카테고리의 다른 글
| Box Plot (0) | 2022.04.16 |
|---|---|
| Scatter Plot (0) | 2022.04.14 |
| Run Sequence Plot / Lag Plot (0) | 2022.04.14 |
| Probability Plot / Normal Probability Plot (0) | 2022.04.14 |
| skewness(왜도) / kurtosis(첨도) (0) | 2022.04.14 |