Probability Plot
4가지 기본 가정 중 고정분포 가정 테스트에 이용
데이터셋이 근사적으로 주어진 분포를 따르는지에 대한 가정을 검사하기 위해 사용하는 Plot
이론상 분포에 대해 데이터를 그리고, 그림이 직선에 가까우면 데이터가 근사적으로 그 분포를 따름
직선 형태에서 멀어질수록 특정 분포의 모양과 데이터의 모양이 다르다는 뜻
ex) weibull 분포를 따르는 데이터셋
rv_weibull = stats.weibull_min.rvs(1.5, size=10000)
sns.histplot(rv_weibull, bins=50, stat='density', kde=True)
stats.probplot(rv_weibull, dist=stats.weibull_min, sparams=(1.5),plot=plt)결과값

가능한 질문들
주어진 분포가 내 데이터셋과 잘 맞는지
내 데이터에 가장 적합한 분포는 무엇인지
선택한 분포의 위치 및 척도 추정치
Normal Probability Plot = QQ plot
* QQ plot : 수집 데이터를 표준정규분포 분위수와 비교해서 그리는 그래프
Probability Plot 의 특별한 경우
데이터셋이 근사적으로 정규분포를 따르는지 판단
그림이 직선에 가까우면 데이터가 근사적으로 정규분포를 따르고,
직선에서 멀어질수록 정규성에서 이탈
가능한 질문들
데이터가 정규분포를 따르는지, 정규성에서 벗어나는 특징이 있는지 : ex) 치우침, 예상보다 짧은/긴 꼬리
code ex)
# 데이터: 195 samples from Heat Flow Meter Data (heatflowmeter1.csv)
sns.histplot(df_heat, bins=30, stat='density', kde=True)
stats.probplot(df_heat['Y'], fit=True, plot=plt) # default: N(0,1)결과값

Normal Probability Plot 의 여러 형태
1. 정규분포 데이터

강한 선형 패턴, 정규분포가 적합한 데이터
2. 꼬리가 짧은 데이터
(short tail = platykutric = kurtosis 값이 작음)

비선형 패턴 -> 정규분포가 적합하지 않음
좌측 꼬리 : 선 위쪽으로 멀어짐
우측 꼬리 : 선 아래쪽으로 멀어짐
3. 꼬리가 긴 데이터
(long tail = Leptokurtic = kurtosis 값이 큼)
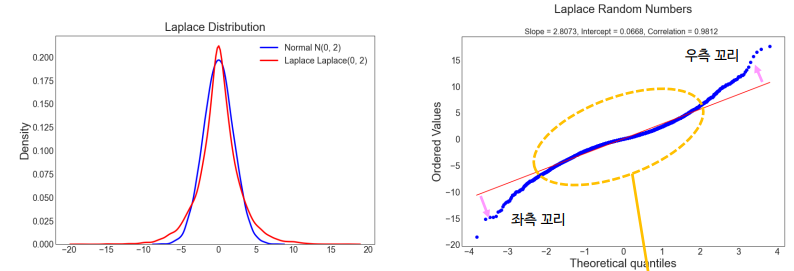
비선형 패턴 -> 정규분포가 적합하지 않음
좌측 꼬리 : 선 아래쪽으로 멀어짐
우측 꼬리 : 선 위쪽으로 멀어짐
4. right-skewed data
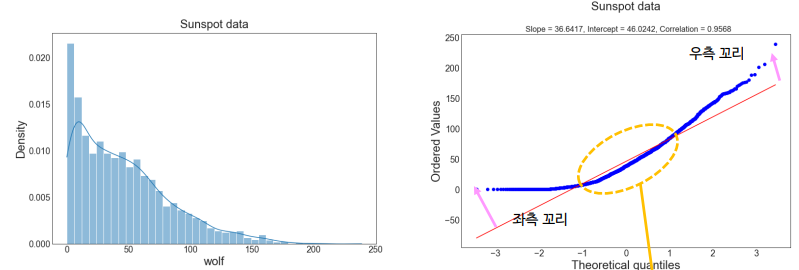
오른쪽 꼬리가 긴 데이터
강한 비선형성
이차곡선 패턴
중간부분이 직선 아래 있고 좌/우측 꼬리는 직선보다 위쪽으로 점점 멀어짐
'School > 데이터사이언스개론' 카테고리의 다른 글
| Box Plot (0) | 2022.04.16 |
|---|---|
| Scatter Plot (0) | 2022.04.14 |
| Histogram (0) | 2022.04.14 |
| Run Sequence Plot / Lag Plot (0) | 2022.04.14 |
| skewness(왜도) / kurtosis(첨도) (0) | 2022.04.14 |