states : representation of a physical configuration
node : search tree를 구성하는 data structure
Tree search algorithms
- expanding states
- successor를 generate하면서(node를 expand 하면서) state space를 탐색하는 것
Tree Based Search strategies
node를 extend 하는 순서에 따라 달라짐
Strategy 평가
- Completeness : solution이 존재하는 경우 항상 찾아주는지
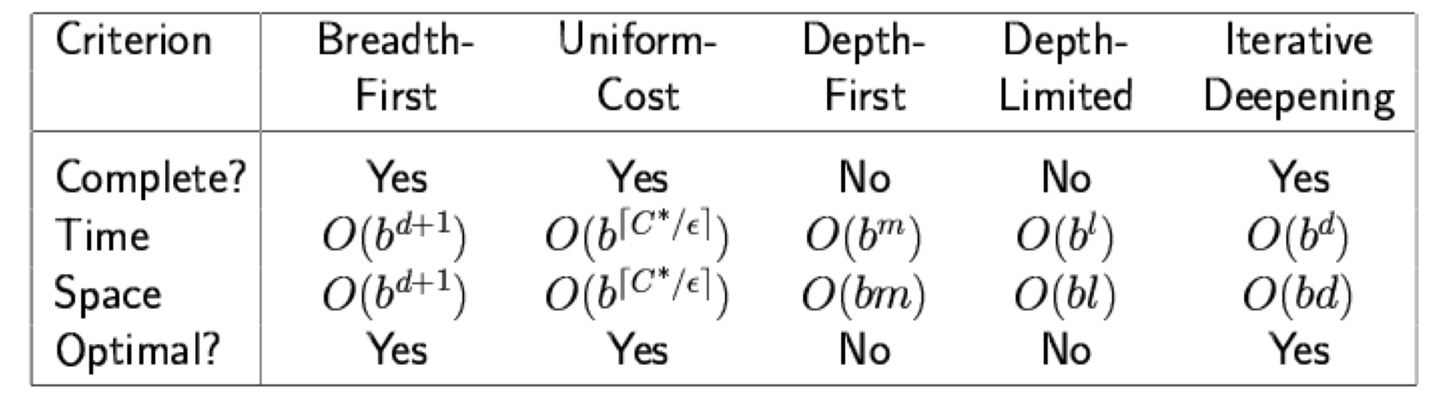
- Time complexity : 탐색에 걸리는 시간 (탐색한 노드의 수, 생성되는 노드 수에 비례) (worst case)
- Space complexity : 요구하는 메모리 (메모리에 저장된 노드의 최대 수에 비례) (worst case)
- Optimality(Quality of solution) : least-cost solution (ex. 최소깊이) 을 항상 찾을 수 있는지
Time/Space complexity 표현
- b : search tree에서 branching factor의 최댓값 (=한 node에 딸린 가지 수)
- ex) root node에서 갈 수 있는 다음 node가 3개 >> b = 3
- d : least-cost solution의 깊이
- ex) root node에서 goal node 까지의 깊이가 3 >> d = 3
- m : state space의 maximum depth (=root node에서 들어갈 수 있는 최대 깊이, ∞도 가능)
Uninformed Search
Use only the information avaliable in the problem definition
사전정보를 갖지 않고 탐색하는 알고리즘 기법, 문제 정의에서 알고있는 정보들만 사용
현재 node에서 goal node까지의 거리(heuristic value)를 알지 못하기 때문에 Blind search라고도 불림
cf. Informed Search : current state에서 goal까지의 estimate distance(heuristic value)를 가짐
Uninformed Search 알고리즘의 종류
- Breadth-First Search
- Uniform-Cost Search
- Depth-First Search
- Depth-Limited Search
- Iterative Deepening Search
1. Breadth-First Search
https://magician-of-c.tistory.com/12
Search Algorithm [2]. 너비 우선 탐색 (Breadth First Search : BFS)
너비 우선 탐색 (Breadth First Search : BFS) 너비 우선 탐색 이란? * 사전적 정의 : 너비 우선 탐색은 맹목적 탐색방법의 하나로 시작 정점을 방문한 후 시작 정점에 인접한 모든 정점들을 우선 방문하
magician-of-c.tistory.com
- expand shallow unexpected node
- 폭넓게 search 하는 방법
- fringe : FIFO queue (new successors go at end)
BFS의 Performance
- completeness : Yes
- b가 유한한 경우에만 성립
- b가 무한한 경우 폭이 무한히 늘어나 solution 못찾을수도 있음
- Time complexity : O(b^(d+1))
- space complexity : O(b^(d+1))
- Optimality : Yes
- 모든 node를 다 훑어보므로 보장 가능

time complextiy로 인한 수행시간보다도 space complexity가 커서 memory requirements가 큰게 진짜 문제
(메모리는 한정되어있기 때문에)
장점 : Optimal 보장 가능
단점 : 메모리
2. Uniform-Cost Search
- expand least-cost unexpended node
- 가장 얕은 node를 expand하는 대신, 가장 적은 path cost g(n)을 갖는 node n을 expand
- fringe에 frontier를 저장하여 수행
- fringe : g(n)에 의해 정렬되는 priority queue
- frontier : 아직 탐색하지 않은 node의 집합
- 모든 cost가 동일한 경우 BFS와 동일
UCS의 Performance
cost를 이용해서 탐색하므로 b나 d로 복잡도 표현 어려움
- ε : cost가 가장 적은 action의 cost
- C : 최적 경로까지의 Cost
- completeness : Yes (모든 step의 cost>= ε 인 경우)
- Time complexity : O(b^{(C/ε)+1})
- ε = 1, C = d 인 경우 -> O(b^(d+1))
- space complexity : O(b^{(C/ε)+1})
- Optimality : Yes
- 항상 cost가 가장 작은 node를 선택하므로
3. Depth-First Search
https://magician-of-c.tistory.com/10
Search Algorithm [1]. 깊이 우선 탐색 (Depth First Search : DFS)
깊이 우선 탐색 (Depth First Search : DFS) 깊이 우선 탐색 이란? * 사전적 정의 : 깊이 우선 탐색은 맹목적 탐색방법의 하나로 탐색트리의 최근에 첨가된 노드를 선택하고, 이 노드에 적용 가능한 동작
magician-of-c.tistory.com
- Expand deepest unexpanded node
- fringe : LIFO queue (put successors at front)
- 원하는 해를 찾기 위해서 전진할 수 있을 때까지 전진
- 어떤 Version을 사용하는가에 따라서 특성이 서로 다른데, 이 글에서는 Tree-Search Version을 다룸
DFS의 Performance
- completeness : No
- b가 유한한 경우에만 성립
- b가 무한한 경우 폭이 무한히 늘어나 solution 못찾을수도 있음
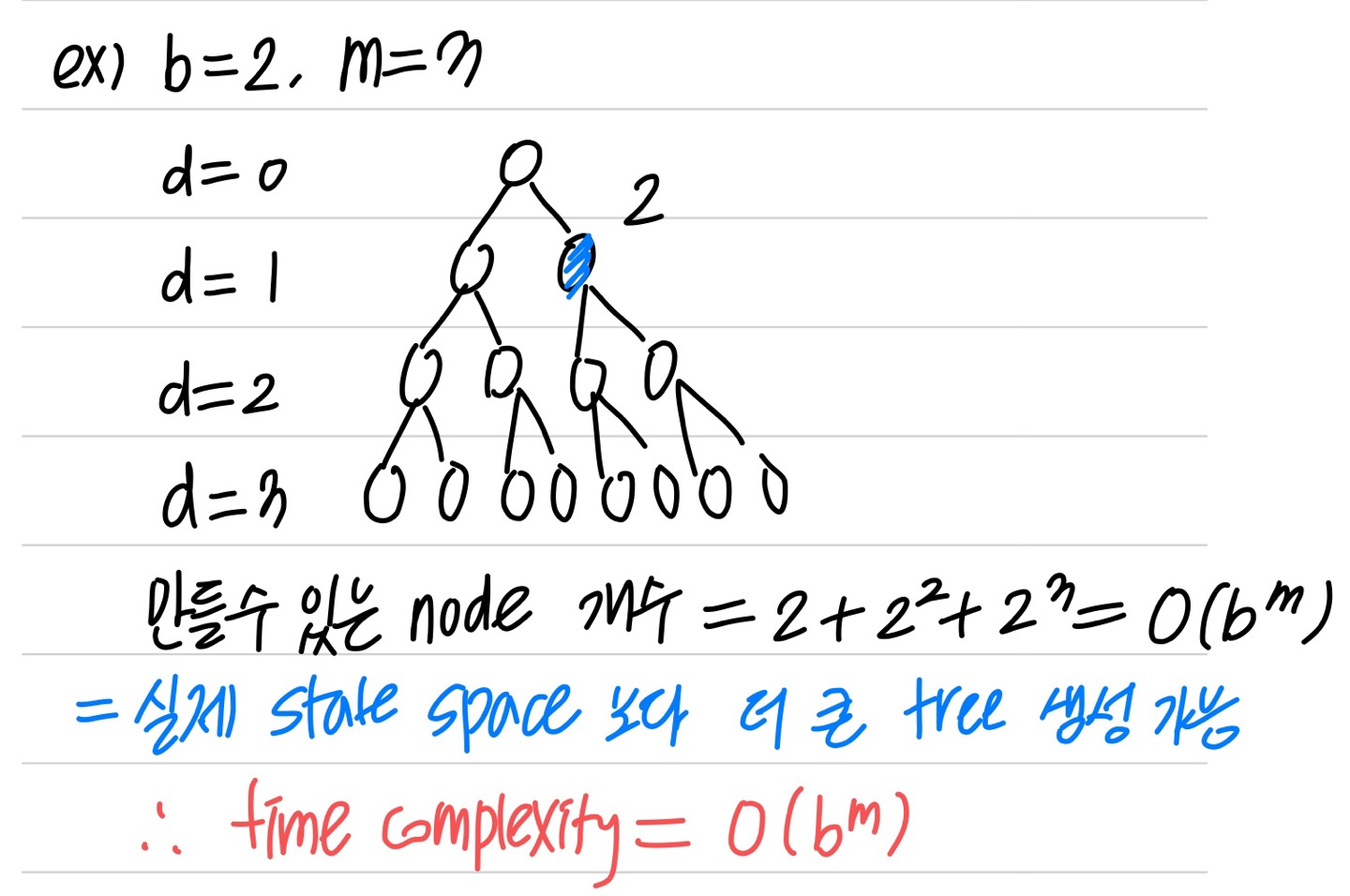
- Time complexity : O(b^m)
- state space의 갯수에 영향을 받음
- space complexity : O(bm)
- root node부터 말단까지 expand 된 이후 더이상의 자식 노드가 존재하지 않는다면 메모리에서 지워버리면 됨
- root부터 leaf까지 1개 path만 저장하면 됨
- state space에서 자식 node가 b개 있고, 최대 깊이가 m이라고 한다면 node 개수는 O(bm) 개만 필요
- Optimality : No
- 끝까지 탐색하다가 Goal-node가 나오면 중단하는 방식
- 그옆의 더 얕은 node에서 답이 나올 수 있지만 확인하지 않으므로
장점 : BFS에 비해 메모리 소요가 적음
단점 : Optimal 보장 불가능, Search tree에서 매우 깊지만 해가 해당 깊이에 없는 경우를 만나게 되면 깊이 빠져들어갈 수 있어 메모리에 문제가 생길 수 있음
4. Depth-Limited Search
- depth의 limit을 l로 설정
- depth l까지 도달하면 더이상의 자식 노드는 존재하지 않는다고 간주하는 알고리즘
- depth l에 있는 node는 sucessor 없음
DLS의 Performance
- completeness : No
- l < d 인 경우 not complete
- Time complexity : O(b^l)
- space complexity : O(bl)
- Optimality : No
- l > d 인 경우 DFS와 동일
5. Iterative Deepening Search
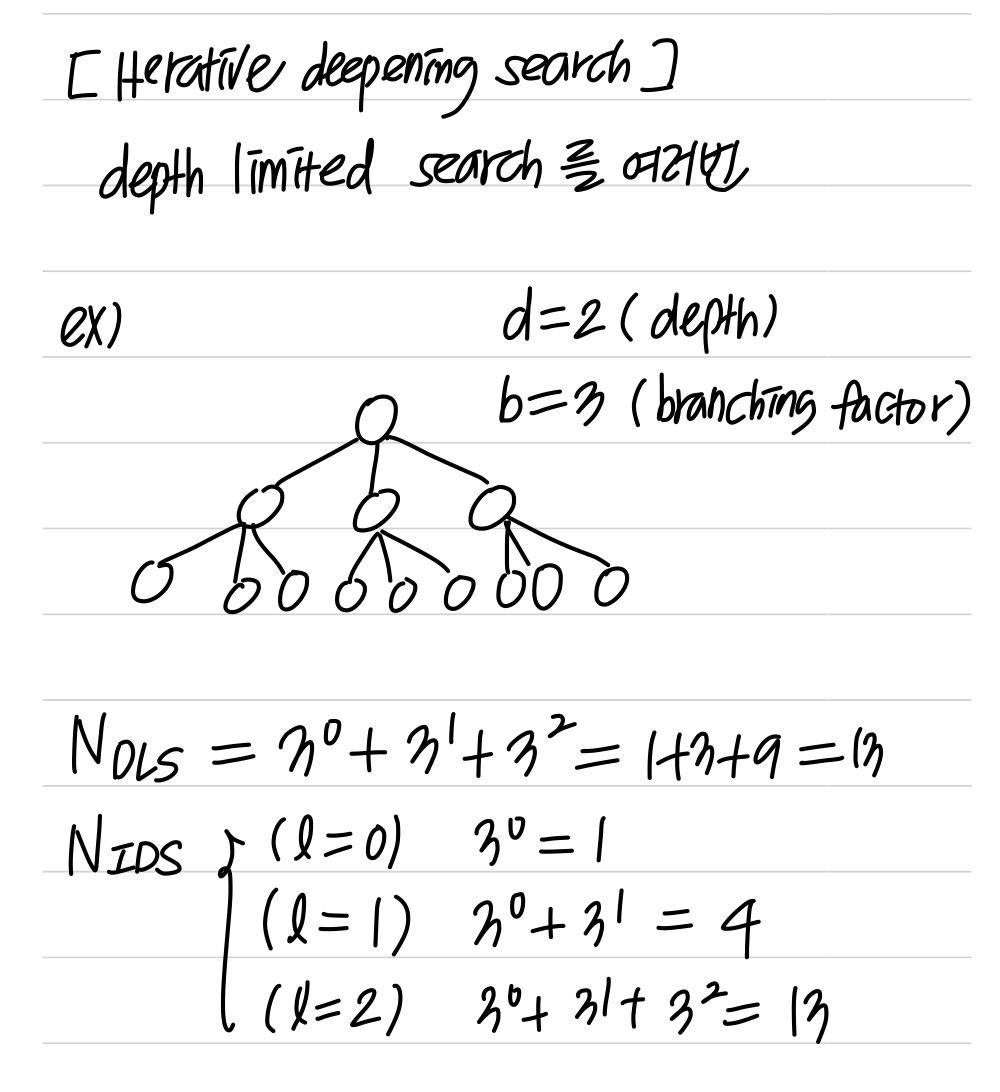
- 반복적인 깊이 탐색
- DFS랑 조합하여 사용되는 Strategy
- 점차적으로 depth limit을 증가하여 최적의 depth limit 값을 찾을때까지 진행
- 알고리즘상 Depth limit 값이 d(Shallowest goal node의 depth)에 도달할때까지
- DFS와 BFS의 장점을 조합한 알고리즘
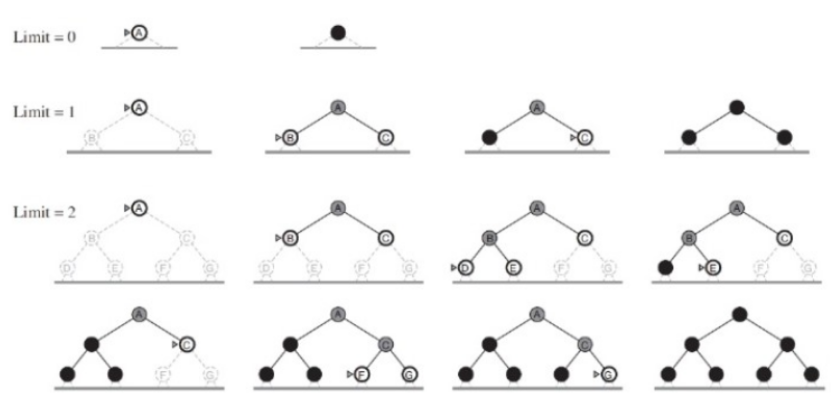
DLS와 lterative deepening search 비교
Depth Limited Search vs. Iterative Deepening Search
DLS에서 만들어지는 node의 수 = b^0 + b^1 + ... b^d
IDS에서 만들어지는 node의 수 = (d)b + (d-1)b^2 + (d-2)b^3 + ... + (1)b^d -> O(b^d)
DLS와 IDS의 overhead 비교
-> IDS의 performance가 우수함을 알 수 있음

IDS의 Performance
- completeness : Yes
- Time complexity : O(b^d) : least cost solution이 있는 깊이까지 node를 만듦
- space complexity : O(bd) : 한 depth에 있을 수 있는 node 개수*least cost solution의 깊이
- Optimality : Yes (step cost = 1 인 경우) : least cost solution 깊이까지 탐색하므로
Summary
'School > 인공지능입문' 카테고리의 다른 글
| 4-4. logic_Theorem proving, Resolution, Forward and Backward Chaining (0) | 2023.04.24 |
|---|---|
| 4-3. Logic-syntax, semantics, Truth Table (0) | 2023.04.24 |
| 4-2. Logic-entailment, model (0) | 2023.04.24 |
| 4-1. Logic-KB, Wumpus world (0) | 2023.04.24 |