머신러닝_실습_3장_선형회귀분석

머신러닝의 목적 

실 데이터를 바탕으로 모델을 생성

데이터 외의 다른 값을 넣었을 때 발생할 아웃풋을 예측

 

선형회귀 

데이터를 가장 잘 설명할 수 있는 선을 찾아내는 것 

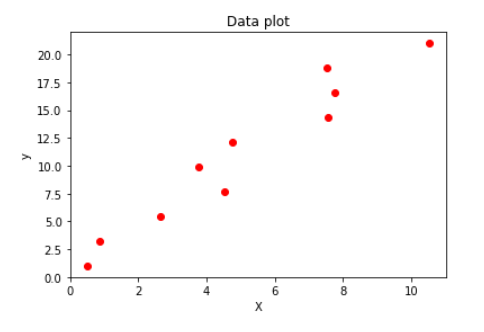
식물에 대한 dataset 이라고 생각해보자.

x축이 나이, y축이 키라고 했을때 해당 dataset 을 잘 설명할 수 있는 선을 하나 만든다면 같은 종의 새로운 식물에 대한 나이 data를 입력했을때 나이에 맞는 키를 예측 가능할 것이다.

 

 

sample data 형성

# 임의의 샘플 데이터 생성
# y = 2x + 1 + e
np.random.seed(42)

x = [int(i) + np.random.randn(1) for i in np.linspace(0, 10, 10)]
y = [2 * i + 1 for i in np.linspace(0, 10, 10)]
plt.title('Data plot')
plt.xlabel('X')
plt.ylabel('y')
plt.scatter(x, y, color='red')
plt.show()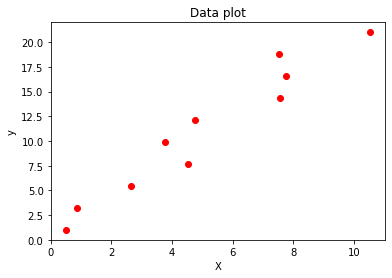

 

sklearn LinerRegression 

#머신러닝에 필요한 라이브러리인 싸이킷런 불러오기
from sklearn.linear_model import LinearRegression

#reg 변수에 LinearRegression 모델을 생성한 후, model 변수에 reg 이용해서 x,y 데이터를 fit 시키기
##fit() : 선형회귀모델에 필요한 두가지 변수(단순선형회귀:기울기, 절편) 를 model에 전달하는 것
reg = LinearRegression()
model = reg.fit(X, y)

#기울기 : model.coef_ / 절편 : model.intercept_
#반올림 하고싶은 경우 : np.round 이용
print(f'Coef : {np.round(model.coef_, 0)} \nIntercept : {np.round(model.intercept_, 0)}')

#예측결과 : predict
# x = 15, y = ?
model.predict([[15]])

단순 회귀모형 visualization

 

from sklearn.linear_model import LinearRegression
#pandas : 데이터프레임 처리
import pandas as pd
#numpy : 수치 데이터 처리
import numpy as np
#matplotlib : 시각화
from matplotlib import pyplot as plt
from sklearn import datasets

#title : 제목
plt.title('Simple Linear Regression')

#xlabel('x축이름')
plt.xlabel('X')
plt.ylabel('y')

#scatter : 산점도
plt.scatter(x, y, color = 'red')

#plot(x축 값, y축 값)
plt.plot(x, model.coef_* x + model.intercept_)

#text(x좌표, y좌표, 텍스트)
plt.text(1, 1, 'y = ' + str(np.round(model.coef_[0], 0)) + 'x + ' + str(np.round(model.intercept_, 0)) )

plt.show()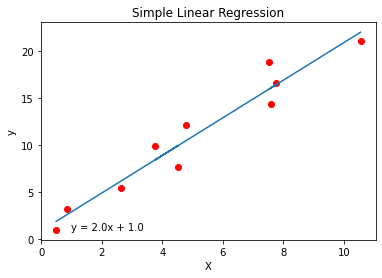

실제 데이터에 적용_데이터셋 고찰

from sklearn.datasets import load_diabetes
'''
Diabetes dataset

-- X : 당뇨병 환자 442명에 대한 '나이', '성별', 'bmi', '혈압' 등 10 가지의 정보
-- y : 당뇨병 진행도
'''

dataset = load_diabetes()

#dataset에서 data와 target 을 matrix 또는 vector 형태로 분류
X = dataset.data
y = dataset.target

# Feature matrix, target vector의 shape 확인
print(f'X shape : {X.shape}')
print(f'y shape : {y.shape}')

# Feature matrix의 각 feature 이름 확인
print(f'Features : {dataset.feature_names}')

X shape : (442, 10)

y shape : (442,)

Features : ['age', 'sex', 'bmi', 'bp', 's1', 's2', 's3', 's4', 's5', 's6']

#dataframe 만들어서 dataframe 형태로 보기
#pd.Dataframe(데이터, column 이름)
df = pd.DataFrame(X, columns = dataset.feature_names)
df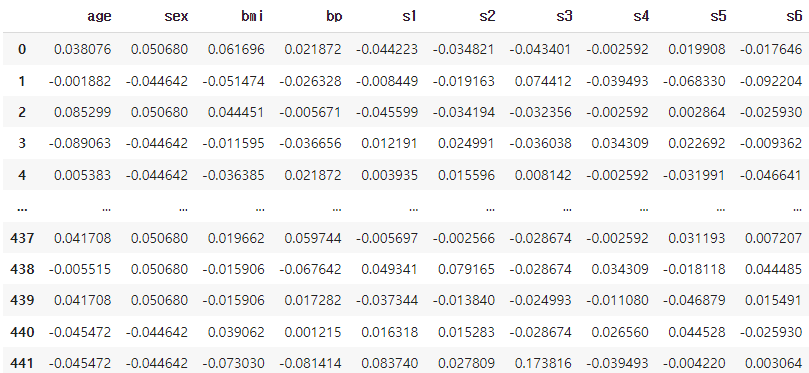

 

 

BMI 이용한 단순 선형회귀

y=a∗bmi+b

# Data plot

#df에서 bmi 열을 array 형태로 추출
bmi = df.bmi.array

plt.title('BMI vs Diabetes progression')
plt.scatter(bmi, y) # y : target
plt.xlabel('BMI')
plt.ylabel('Progression')
plt.show()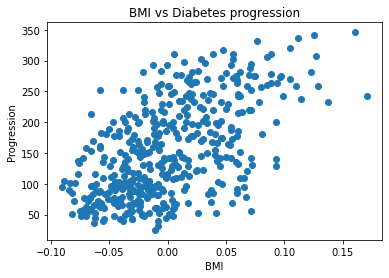

# Linear model Fit
reg = LinearRegression()
#bmi를 -1부터 1까지 범위로 reshape 한 값과 progression(y) 를 선형회귀모델 이용해서 fit 시킴
model = reg.fit(bmi.reshape(-1, 1), y)
print(f'Coef : {model.coef_} \nIntercept : {model.intercept_}')

Coef : [949.43526038]

Intercept : 152.1334841628967

# Linear model plot

plt.title('BMI vs Diabetes progression')
plt.scatter(bmi, y)
plt.xlabel('BMI')
plt.ylabel('Progression')
plt.plot(bmi, pred, color='red')
#model 의 score
plt.text(0.1, 200, '$R^2$ = ' + str(model.score(bmi.reshape(-1, 1), y)))
plt.show()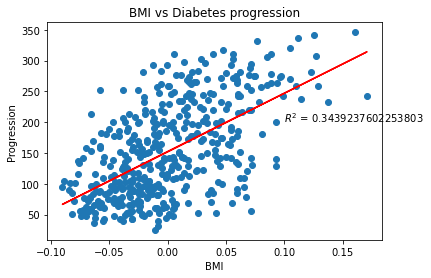

모든 feature 사용한 다중 선형회귀

y=α∗X+β

# Linear model Fit

reg = LinearRegression()
model = reg.fit(X, y) #X : 모든 feature
print(f'Coef : {model.coef_} \nIntercept : {model.intercept_}')
pred = model.predict(X)

Coef : [ -10.01219782 -239.81908937 519.83978679 324.39042769 -792.18416163 476.74583782 101.04457032 177.06417623 751.27932109 67.62538639]

Intercept : 152.1334841628965

# Linear model plot

a = np.linspace(25, 300)
plt.plot(a, a, color='red')
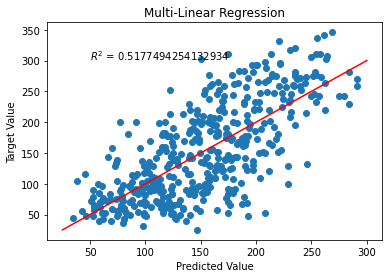
plt.title('Multi-Linear Regression')
plt.scatter(pred, y)
plt.xlabel('Predicted Value')
plt.ylabel('Target Value')
plt.text(50, 300, '$R^2$ = ' + str(model.score(X, y)))
plt.show()