알고리즘이란 ?
어떤 과제를 완수하기 위한 절차/단계/규칙
머신러닝 알고리즘?
예측, 분류, 군집화. 차원축소 등에 이용
분류문제 혹은 예측문제
| 선형 회귀 알고리즘 | k-근접이웃 알고리즘 | k-평균 알고리즘 |
| 지도학습, 예측 | 지도학습, 분류 | 비지도학습, 군집화 |
선형회귀
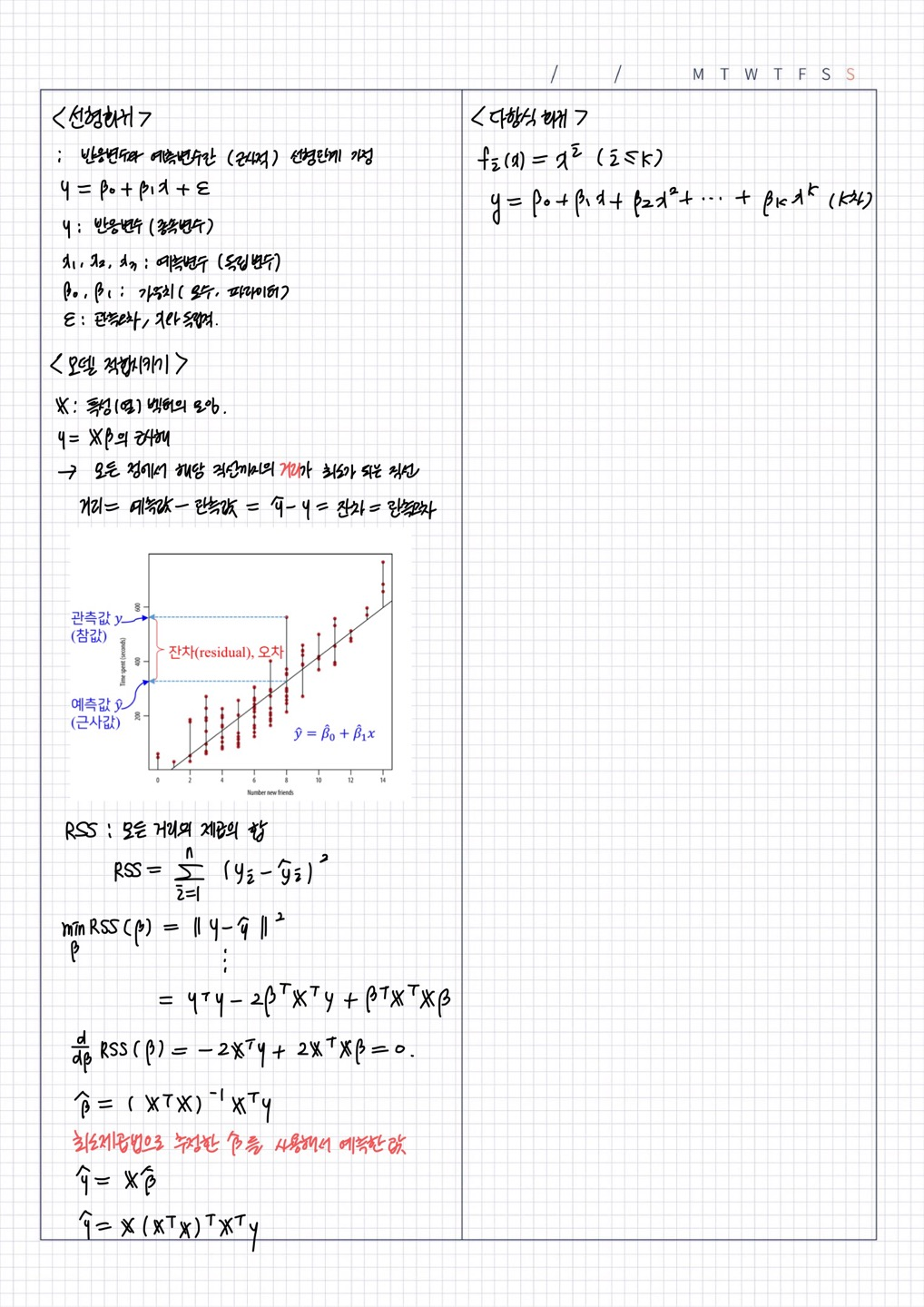
과적합과 미적합

| 용어 | 과적합 | 미적합 |
| 설명 | 모델이 학습 데이터에 대해서는 좋은 성능을 보이지만, 처음 보는 새로운 데이터에 대해서는 성능이 나빠지는 현상 (잘 일반화되지 않는 현상) | 모델이 너무 단순해서 학습데이터조차 부적합 |
| 발생원인 | 학습 데이터 양과 노이즈 정도에 비해 모델의 복잡도가 너무 클 때 모델의 복잡도에 비해 데이터가 너무 적을 때 학습 데이터를 기억하기 시작함 |
- |
| 해결책 | 데이터를 더 수집 더 단순한 모델 사용 데이터 특성 수 줄이기 규제 적용 ** 정규화 ! |
모델 복잡도 늘리기 모델의 제약조건 완화 |
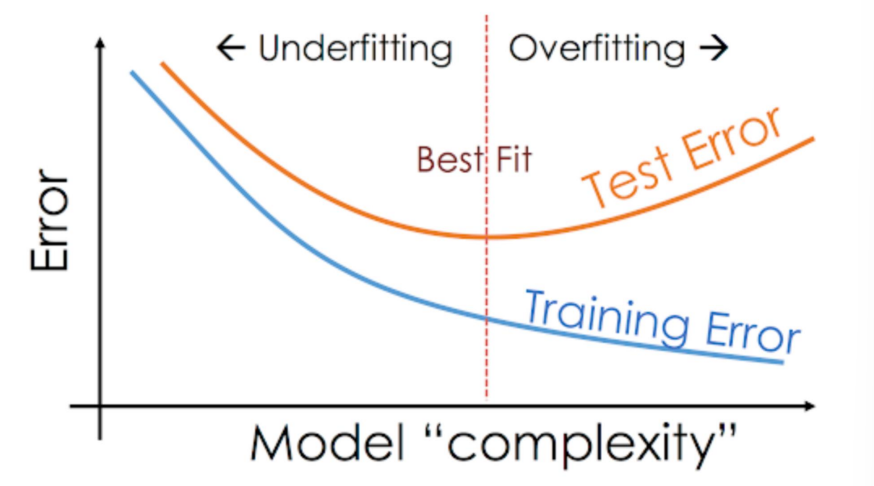
test error = training error + generalization gap
generalization gap = test error - training error
* test error : 학습에 사용하지 않고 따로 빼둔 data 를 이용해서 구한 값
1) training error 가 커서 test error 가 큰 경우 = 과소적합 => 모델의 복잡도를 늘려서 개선시켜야
2) generalization gap 이 커서 test error 가 큰 경우 = 과적합 => 모델의 복잡도를 낮춰서 개선시켜야
모델의 평가측도
1. R제곱값

1에 가까울수록 좋은 모델, 0에 가까울수록 나쁜 모델
-> 오차 > 편차 면 평균값으로 예측한것보다 별로인 모델이라는 뜻
2. p-값
3. 교차검증
1) 데이터를 training set: test set 으로 구분 ( 보통 8:2 )
2) test set 으로 모델 적합시키고, test set MSE와 training set MSE 비교
3) MSE 가 비슷하면 일반화가 잘된 모델
오차를 반영한 선형회귀 모델

오차항 = 실제값 - 예측값
오차항은 정규분포를 따른다고 가정

과적합 문제 해결을 위한 정규화
: Ridge Regression

β : 회귀계수
1) (오차)^2을 최소화하는 β 구하기
2) (회귀계수)^2의 합을 최소화하는 β 구하기
1) 을 줄이기 위해 2) 를 너무 크게 만드는것을 방지하는 penalty term 추가
회귀계수가 너무 발산하지 않는것이 중요할수록 λ 커짐
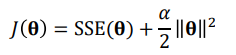
SSE = 비용함수 : 훈련 셋에 있는 모든 샘플에 대한 손실의 합

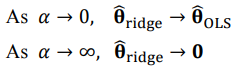
OLS : 최소제곱법
회귀계수가 너무 발산하지 않는것이 중요할수록 α 커짐

OLS estimator 의 해가 항상 존재하는 것은 아님
design matrix X가 full rank(모든 열이 독립)이 아닌 경우 XTX의 역행렬이 존재하지 않음
<-> desgin matrix 가 full rank 인 경우 XTX 역행렬이 존재함
XTX + aI 는 항상 역행렬이 존재하기 때문에 유일해가 존재
OLS 방법보다 항상 Rigde 를 사용한 해가 더 우수(더 작은 MSE 존재)
Lasso Regression

중요하지 않은 feature 들의 parameter 를 완전히 0으로 만드는 경향이 있음
-> feature 선택의 효과, sparse model 만들어줌
절댓값 성분때문에 미분 불가능
'School > 데이터사이언스개론' 카테고리의 다른 글
| 알고리즘-2 (0) | 2022.04.24 |
|---|---|
| Scatterplot Matrix / heatmap (0) | 2022.04.16 |
| Quantile-Quantile Plot(Q-Q plot) (0) | 2022.04.16 |
| Bihistogram (0) | 2022.04.16 |
| Box Plot (0) | 2022.04.16 |